Grammatiche formali, 26/10/22

Table of contents

  1. Introduzione
  2. Parse Tree
  3. Ambiguità di una Grammatica
  4. Derivazioni canoniche
  5. Altri problemi
  6. Esercizi svolti

1 Introduzione

Per prima cosa, viene introdotto il concetto di grammatiche equivalenti:

\(\blacktriangleright\) Due grammatiche sono equivalenti se generano lo stesso insieme di stringhe, quindi se definiscono lo stesso linguaggio.

Lo scopo del programmatore è quindi quello di scegliere una grammatica che possa agevolare il compito del parser di interpretare le sequenze di token. Esempio di grammatiche equivalenti: \(\downarrow\)

1.1 G1

\begin{equation} E \rightarrow E+E|E\times E \\ E \rightarrow (E)|number \end{equation}

1.2 G2

\begin{aligned} & E \rightarrow E+T | T \\ & T \rightarrow T \times F | F \\ & F \rightarrow number | (E) \end{aligned}

Per rendersene conto, basta fare delle prove semplici, ad esempio convertire \(num \times (num + num)\)

2 Parse Tree

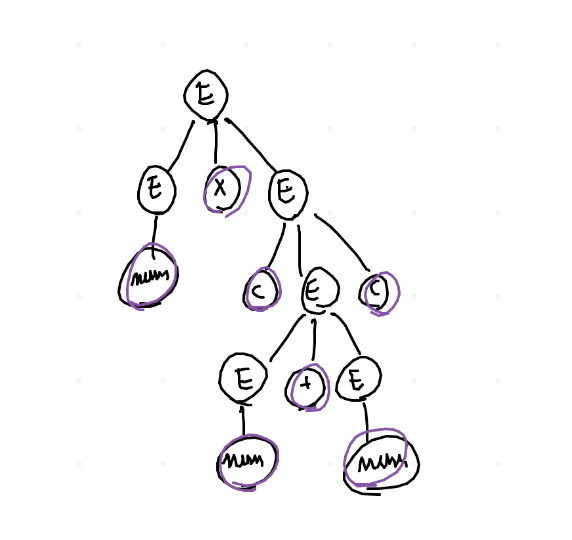
Il Parse Tree è una struttura dati che descrive il processo di derivazione che porta alla stringa finale, come quello in figura \(\downarrow\) tree.png

Una visita DFS in order permette di "leggere" la sequenza finale di interesse, le cui parti sono situate nelle foglie dell'albero.

3 Ambiguità di una Grammatica

Diversi processi di derivazione (usando una stessa grammatica) possono portare alla costruizione di Parse Tree differenti. In questo caso, la grammatica è detta ambigua.

\(\blacktriangleright\) Una grammatica si dice ambigua se almeno una frase ammette diversi Parse Tree.

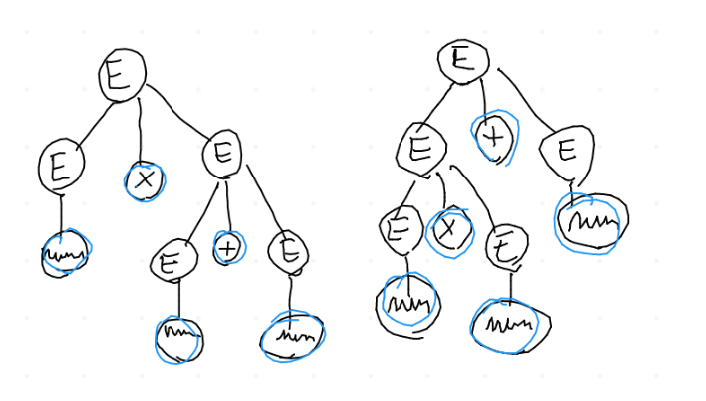
Questo non sarebbe un problema per quanto visto fino ad adesso, ma bisogna pensare al parse tree come un'anticipazione del significato della stringa". Ciò significa che alcuni alberi potrebbero risultare "sbagliati" dal punto di vista interpretativo. Ad esempio: \(\downarrow\) ambig.png

\begin{equation} num \times num + num \end{equation}

in questo caso, l'albero di sinistra "sembra scorretto", perchè suggerisce l'esecuzione dell'addizione (che si trova nel blocco più basso) rispetto all'esecuzione della moltiplicazione, che invece ha la precedenza. Una grammatica non ambigua, al contrario, forza l'esistenza di una sola derivazione, quindi la costruzione di un solo albero!

4 Derivazioni canoniche

Un processo utile per aiutare la "regolarizzazione" di una grammatica, è quello di definire una specifica derivazione da utilizzare. Solitamente si hanno 2 scelte:

  1. Derivazione canonica destra;
  2. Derivazione canonica sinistra;

\(\blacktriangleright\) Una derivazione canonica destra/sinistra prevede ad ogni passo la riscrittura del simbolo non terminale più a destra/sinistra

In questo modo, dato un parse tree, si riesce sempre a risalire al processo di derivazione utilizzato!

5 Altri problemi

Altri problemi che possono ostacolare il ruolo del parser sono:

  • Cicli: \(A \overset{+} \Rightarrow A\);
  • Left recursion: \(A \overset{+} \Rightarrow A\alpha\);
  • Prefissi comuni; \(A \rightarrow \alpha\beta_{1}\) e \(A \rightarrow \alpha\beta_{2}\)

problems.png

I problemi riguardo le precedenze di operatore prima sollevati possono essere risolti aggiungendo dei "layer" alla grammatica, secondo i livelli di precedenza. Ad esempio:

\begin{aligned} & E \rightarrow E + T \ | \ T \\ & T \rightarrow T \times F \ | \ F \\ & F \rightarrow number \ |\ (E) \\ \end{aligned}

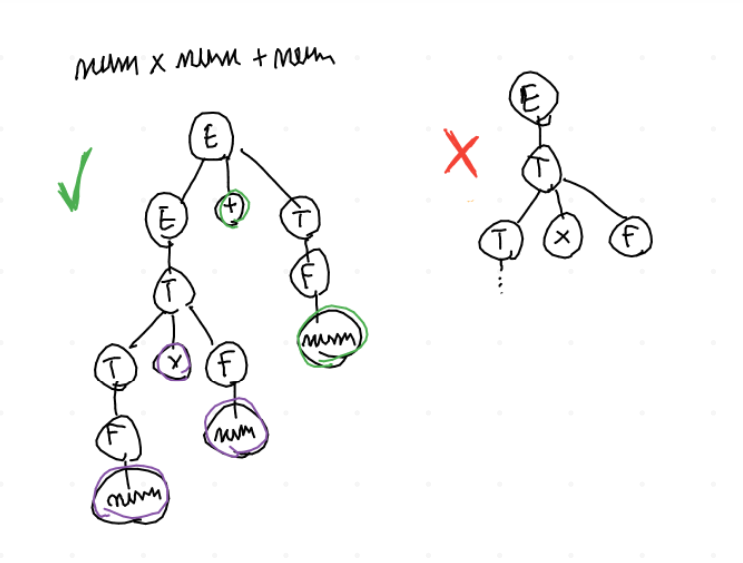
Per ottenere la solita espressione \(num \times num + num\) si può usare soltanto una specifica serie di derivazioni, che oltretutto produce un risultato facilmente interpretabile dal parser. Se si prova a seguire un'altro ordine, ci si blocca subito! cases.png

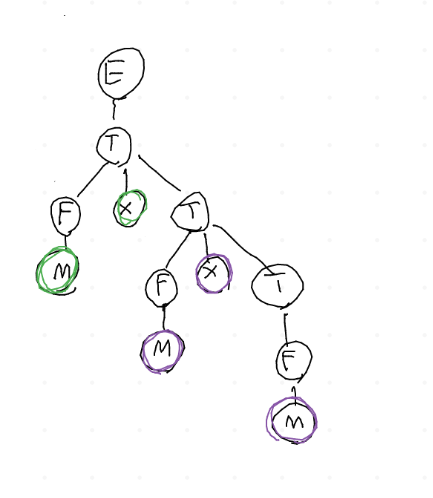
Se usassimo \(T \rightarrow F \times T\) invece di \(T \rightarrow T \times F\), per ottenere \(num \times num \times num\), si otterrebbe un'albero come in figura, che suggerisce un'associatività delle operazioni a destra, quando invece nell'aritmetica si svolgono prima le operazioni sulla sinistra quando esse sono sullo stesso livello di priorità. inversion.png

6 Esercizi svolti

Entrambe le consegne degli esercizi si possono trovare a slide 38 del blocco sulle grammatiche.

6.1 Esercizio 1

Fornire una grammatica libera per l’insieme delle stringhe costituite da parentesi correttamente bilanciate;

\begin{equation} S \rightarrow (S)S \ | \ \epsilon \end{equation}

E' interessante notare il fatto che non esiste alcun automa che possa riconoscere questo tipo di linguaggio, dato che richiede la memorizzazione di sequenze di parentesi.

Forniamo ora una dimostrazione formale per induzione, suddivisa in 2 parti.

6.1.1 Parte 1

Si consideri una generica stringa \(f\) di caratteri non terminali e un generico numero di passaggi di derivazione \(n\).

  • Hp: \(f\) generabile a partire da S;
  • Th: \(f\) è bilanciata;

Ipotesi Induttiva: Se si considera n = 1, l'unica stringa di caratteri non terminali generabile è la stringa vuota, che sicuramente è anche bilanciata.
Induzione: supponiamo che tutte le derivazioni con meno di n passaggi siano in grado di generare stringhe di parentesi bilanciate. (Se può aiutare, al primo passaggio si può considerare \(n=2\), e come abbiamo dimostrato la base induttiva è vera per \(n=1\)). Scriviamo quindi una generica derivazione in \(n\) passaggi:

\begin{equation} S \rightarrow S_{1}(S_{2}) \rightarrow ...x(S_{2}) \rightarrow ...x(y) \end{equation}

dove \(x\) e \(y\) indicano delle sequenze di caratteri terminali. Dato che l'intera produzione è lunga \(n\) passaggi, si sa per certo che le derivazioni che hanno portato alla riscrittura di \(S_{1}\) in \(x\) e di \(S_{2}\) in \(y\) sono lunghe meno di n passaggi. Quindi per ipotesi induttiva le stringhe \(x\) e \(y\) saranno bilanciate. Ma se \(x\) e \(y\) sono bilanciate, allora anche \(x(y)\) lo è \(\square\).

6.1.2 Parte 2

Nella seconda parte della dimostrazione si vuole dimostrare l'inverso, quindi:

  • Hp: \(f\) è una stringa costituita da parentesi bilanciate;
  • Th: \(f\) è sicuramente ottenibile a partire da S;

Ipotesi Induttiva: se si considera una stringa di lunghezza pari a \(0\), essa è sicuramente bilanciata, e di sicuro è ottenibile da S dato che si tratta di ε.
Passo induttivo: si consideri una generica stringa \(w\) lunga \(2n\) caratteri ( si usa \(2n\) perchè le parentesi bilanciate sono ovviamente costituite da un numero pari di parentesi). Presupponiamo che tutte le stringhe di lunghezza minore di \(2n\) siano ottenibili a partire da \(S\).

Dato che \(w\) è bilanciata, può sicuramente essere riscritta come \(x(y)\), dove \(x\) e \(y\) sono a loro volta bilanciate e di lunghezza sicuramente minore della lunghezza totale di \(w\), che è \(2n\). Per ipotesi induttiva esse sono quindi ottenibili a partire da \(S\). Ma se questo è vero, posso allora scrivere questa produzione:

\begin{equation} S \rightarrow S(S) \rightarrow ...x(S) \rightarrow ...x(y) \end{equation}

e leggendo soltanto il primo e ultimo termine

\begin{equation} S \rightarrow x(y) = w \ \square \end{equation}

6.2 Esercizio 2

Fornire una grammatica libera per il linguaggio \(L_{1,2}=\{a^nb^{2n} | n>=0\}\)

\begin{equation} S \rightarrow aSbb | \epsilon \end{equation}

In questo modo, ogni volta che si aggiunge una \(a\) all'inizio, si aggiungono 2 \(b\) alla fine, creando il linguaggio giusto.