Abstract Syntax Tree construction, 17/11/22

Info

La lezione tratta un'esempio di esecuzione del parser predittivo(ricorsivo) con costruzione dell'AST. E' molto utile per capire a grandi linee il funzionamento del codice.

1 Introduzione

L'abstract Syntax Tree è l'albero che descrive la struttura sintattica di un programma, o di una sequenza di token di input.

A differenza del parse tree, l'AST non contiene caratteri non terminali intermedi, o altri caratteri terminali come le parentesi. Lo scopo dell'AST è descrivere il "significato" del codice tramite la sua stessa struttura.

2 Esempio

Ad esempio, considerando la solita grammatica di riferimento, il parse tree per la semplice l'espressione

\begin{equation} 3+4 \end{equation}

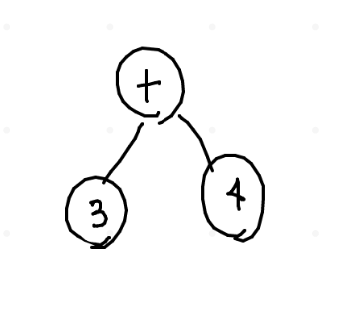
sarebbe il seguente \(\Downarrow\) 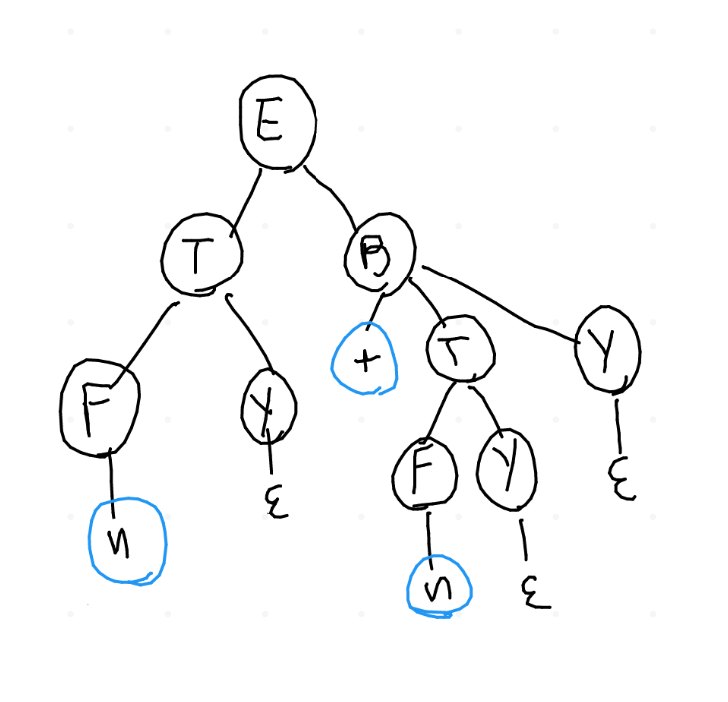ast2.png mentre l'AST sarebbe più semplicemente questo \(\Downarrow\)

ast1.png

3 L'algoritmo

Vediamo ora come il codice costruisce l'AST partendo dal basso. Si tenga sempre sott'occhio anche il parse tree.

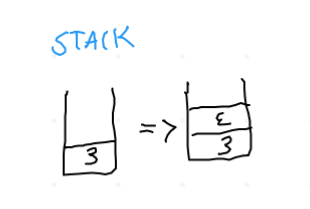
L'idea generale è quella di costruire l'AST facendo uso di uno stack di puntatori ai nodi dell'albero. Man mano, i puntatori all'interno dello stack verranno estratti 2 alla volta per costruire i vari sottoalberi dell'AST. In base al contenuto dello stack in ogni momento, l'aggregazione dei nodi verrà fatta in modo diverso.

Tenere sempre a mente che l'ordine delle chiamate ricorsive sui nodi è il seguente: \(\Downarrow\)

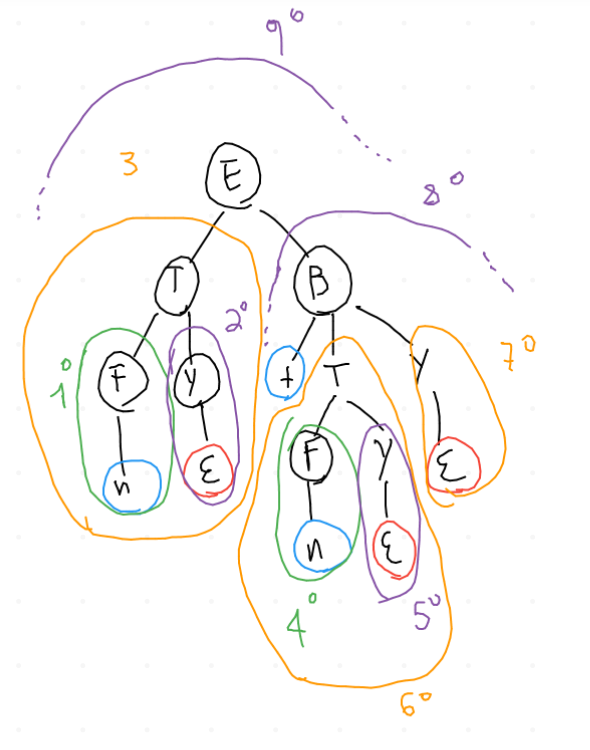
ast3.png

La prima chiamata ricorsiva che si risolve è la N.1: dato che la parte destra della produzione contiene soltanto un terminale e questo ha valore lessicale, viene invocata la funzione che costruisce la foglia e viene inserito nello stack un puntatore ad essa.

La seconda chiamata che si risolve inserisce nello stack un puntatore nullo.

ast4.png

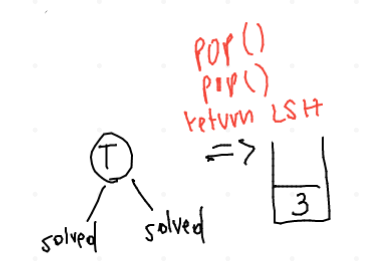
Ora il control flow "torna alla T", che ha risolto i suoi due sottoalberi senza incontrare incongruenze con l'input. Ora il controllo è passato alla funzione che deve creare il sottoalbero (ASTBuild nel file ASTclasslessexpr3.cpp). Lei capisce che è stata chiamata su un nodo interno, quindi su un carattere non terminale. Dato che trova un puntatore nullo sulla cima, semplicemente re-inserisce nello stack l'elemento non nullo. Questa semplificazione permette di eliminare degli elementi "garbage" dall'albero.

ast5.png

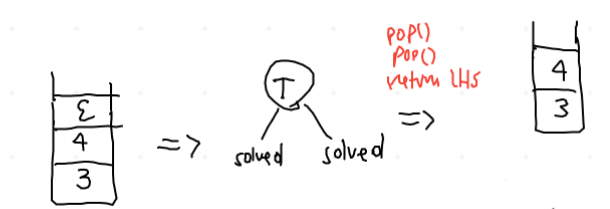
Il codice che descrive questa parte è il seguente: 

else {
	 ExprAST *RHS = AStree.top();
	 AStree.pop();
	 ExprAST *LHS = AStree.top();
	 AStree.pop();
	 if (RHS==nullptr) return LHS;
	 return rotate(LHS,RHS);
   }

La quarta e la quinta chiamata inseriscono semplicemente nello stack il token "4" e un puntatore nullo. Il controllo torna alla sesta chiamata, che esegue esattamente i passi svolti nella terza chiamata.

ast6.png

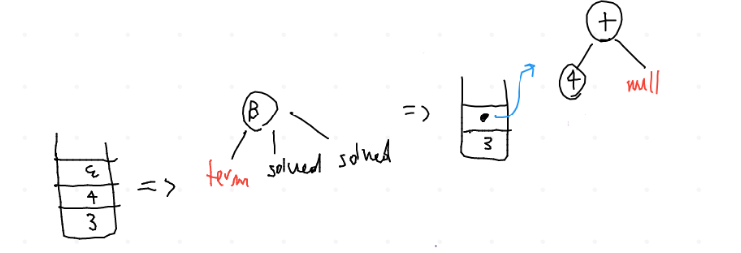
La settima chiamata aggiunge un puntatore nullo. L'ottava chiamata è particolare: la funzione ASTbuild trova un token all'inizio della produzione, quindi entra in questo switch case ed effettua l'aggregazione dei due elementi che trova nello stack (4 e nullpointer). 

ExprAST *ASTBuild(std::vector<int> &prod, int inner) {
  if (inner) {
	int tok = prod.at(0);
	if (isterm(tok)) {
	  switch(tok) {
	  case '+': case '*':
	{
	  auto *RHS = AStree.top();
	  AStree.pop();
	  auto *LHS = AStree.top();
	  AStree.pop();
	  ExprAST *E = new BinaryExprAST(tok,LHS,RHS);
	  return E;
	}

ast7.png

Nell'ultima chiamata il controllo torna ad E, che ha risolto i due sottoalberi senza incontrare problemi. La produzione che viene applicata ad E ha un carattere non terminale all'inizio, quindi la funzione che crea l'albero finisce di nuovo in questa parte di codice: 

else {
	 ExprAST *RHS = AStree.top();
	 AStree.pop();
	 ExprAST *LHS = AStree.top();
	 AStree.pop();
	 if (RHS==nullptr) return LHS;
	 return rotate(LHS,RHS);
   }

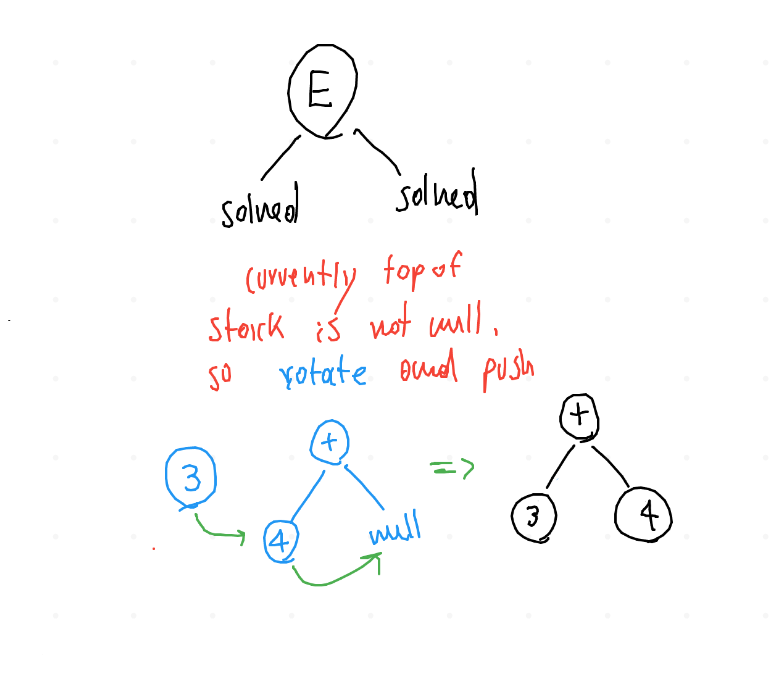
questa volta però in cima allo stack non c'è un puntatore nullo, quindi viene applicata la funzione rotate e viene ritornato il puntatore all'albero risultante. Infatti alla fine della costruzione dell'albero avremo sempre in basso a destra un puntatore nullo. Per correggere questo problema e dare la giusta forma all'AST, si fanno shiftare verso sud-est (basso a sinistra) tutti i nodi per fare spazio ed eliminare il puntatore nullo! 

ExprAST *rotate(ExprAST *First, ExprAST *Rest) {
  printstack();
  ExprAST *top = Rest;
  while (Rest->right() != nullptr) {
	ExprAST *tmp = Rest->left();
	Rest->setval(First,Rest->right());
	First = tmp;;
	Rest = Rest->right();
  }
  Rest->setval(First,Rest->left());
  return top;
}

ast8.png