Modelli di information retrieval 03-11-22/04-11-22(t)
Si cerca di definire un'ordinamento tra i documenti di interesse, in base alla loro rilevanza rispetto alla query inserita. Un modello è definito dalla seguente tripla:
\begin{equation} (D,Q,R(q_{i}, dj)) \end{equation}\(q_{j} \rightarrow\) query;
\(d_{j} \rightarrow\) documento;
\(R(q_{j}, d_{j}) \rightarrow\) funzione che associa un numero reale alla coppia query-documento, in base al suo valore di similarità;
\(\Rightarrow\) La domanda a cui rispondere è: quanto è rilevante il documento rispetto alla query? \(R(q_{j}, d_{j})\) associa un numero reale alla coppia query-documento, per stabilirne la pertinenza! Si introducono ora alcuni concetti fondamentali:
Alcuni motivi per calcolare la similarità:
Classificazione \(\rightarrow\) di oggetti sconosciuti;
Clustering \(\rightarrow\) raggruppare oggetti che si assomigliano;
Query by content \(\rightarrow\) quanto un'oggetto soddisfa le richieste di una query!
Ovviamente nel calcolo della similarità si tiene conto della rappresentazione logica di un documento, che nel nostro caso sono i termini che sopravvivono alla fase di preprocessing. Quindi in realtà si potrebbe calcolare la similarità in base a diverse "feature" \(\rightarrow\) il valore di similarità può cambiare drasticamente in questo caso.
Tendenzialmente questa fase segue questo schema:
Generazione delle features iniziali;
Pulizia delle feature per liberarsi di eventuale rumore;
Normalizzazione delle feature per uniformare i dati;
Riduzione delle feature per essere più efficienti;
Solitamente vengono anche generate nuove features derivate.
Tutti i modelli classici necessitano di una rappresentazione dei documenti su cui lavorare. Ne esistono diverse, ma una delle più diffuse è la bag of index term. Si suppone che la semantica possa essere espressa semplicemente come sequenza di index term, che sono sopravvisuti alla fase di pre-processing. Questa potrebbe essere vista come una "semplificazione", ma al giorno d'oggi è una tecnica rodata e usata anche da search engine complessi come google.
Index term \(\rightarrow\) parole la cui semantica ricorda il tema principale del documento;
Pesi \(\rightarrow\) servono per misurare il ruolo di un termine nella rappresentazione di un documento.
con l'indice \(t\) che scorre su tutti i termini indice del documento \(j\).
Solitamente i pesi vengono considerati come indipendenti. E' un'assunzione semplicistica ma che riduce di molto il lavoro.
\(\Rightarrow\) concetto di Bag of words: l'ordine in cui i termini compaiono nei documenti non viene considerato. Le seguenti due frasi hanno lo stesso vettore dei pesi.
Mary is quicker than John
John is quicker than Mary
E' bene comunque ricordarsi che anche al giorno d'oggi molti sistemi di ricerca che usiamo frequentemente sono booleani, come grep di linux o la ricerca di windows (almeno fino a qualche anno fa).
Le query che consideriamo sono booleane, quindi un documento può soddisfare o no la query data. Si parla quindi di exact matching, non esiste il concetto di similarità. E' stato usato per molti anni all'inizio dell'information retrieval.
In questo caso, si assume quindi che i pesi siano tutti binari. Esempio:
\begin{equation} t_{x} \ AND \ t_{y} = \{d_{i}|w_{ix} = 1\} \cap \{d_{i}|w_{iy} = 1\} \end{equation}Vantaggi
Il formalismo è chiaro, di conseguenza anche la semantica.
Svantaggi:
Non esiste il concetto di ranking --> il rischio è quello di ricadere nell'information overwhelming, oppure usando una query troppo specifica si potrebbero avere pochi risultati. --> example: WestLaw, library in ambito giuridico. E' complesso scrivere delle query
Un servizio che usa ancora un modello booleano è WestLaw, usato principalmente da esperti in ambito legale.
E' il modello più usato al giorno d'oggi, che si basa sulla rilevanza dei documenti rispetto alla query, e li ordina di conseguenza. Il concetto fondamentale è che tutto è un vettore in uno spazio n-dimensionale. Si usano quindi le operazioni dell'algebra lineare su spazi vettoriali.
Esempio --> SMART, sviluppato dagli studenti del Cornell negli anni 60.
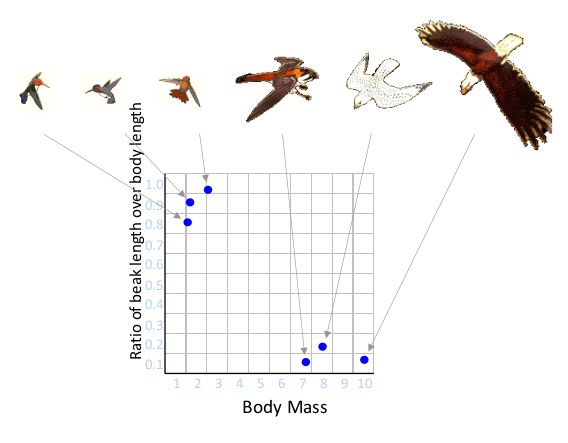
Il concetto è che se viene fornito un nuovo elemento, si calcola la "distanza" tra lui e gli altri punti per capire quali altri elementi sono i più simili.
Dopo aver applicato il pre-processing e aver quindi ottenuto i token, si costruisce un dizionario di \(t\) elementi. A questo punto, i termini diventano gli assi cartesiani. La notazione è la seguente:
\(w_{ij} \rightarrow\) peso del termine i-esimo nel documento j. Se vale 0, semplicemente il termine non è presente.
I documenti e le query ora sono quindi rappresentabili tramite un vettore di pesi di questo tipo:
\begin{aligned} & d_{j} = (w_{1j}, w_{2j}, ... w_{tj}) \\ & q = (w_{1q}, w_{2q}, ... w_{tq}) \end{aligned}Ovviamente questi vettori sono rappresentabili sul piano cartesiano, bisogna capire qual'è il modo migliore per calcolare la distanza!
Per calcolare la distanza tra due vettori, si decide di usare il coseno dell'angolo compreso.
Vettori ortogonali (\(\alpha = 90^o\)) \(\rightarrow\) \(\cos(\alpha)=0\) \(\Rightarrow\) no similarity!
Vettori paralleli (\(\alpha = 0^o\)) \(\rightarrow\) \(\cos(\alpha)=1\) \(\Rightarrow\) max-similarity.
Ma come fare a calcolare il coseno tra i due vettori n-dimensionali? \(\Downarrow\)
La misura del coseno in questo caso è anche detta normalized inner product \(\Downarrow\)
\begin{equation} sim(d_{j}, q) = \frac{d_{j} \cdot q}{|d_{j}| \times |q|} =\frac{\sum_{i=1}^{t}w_{ij} \times w_{iq} }{\sqrt{\sum_{i=1}^{t}w_{ij}^2} \times \sqrt{\sum_{i=1}^{t}w_{iq}^2}} \end{equation}Da notare che la lunghezza della query non influisce sul risultato, mentre la lunghezza del vettore \(\vec{d_{j}}\) serve per normalizzare il risultato (pochi termini in comune, vettori più lunghi \(\rightarrow\) minor similarità). Esempio preso dalle slide: \(\downarrow\)

dato che la lunghezza della query (\(|q|\)) compare in tutte le similarity, non influenza il ranking.
Fino ad ora ci siamo posti in un contesto in cui i documenti sono rappresentati da una lista di pesi binari.
In realtà,i pesi ci dovrebbero permettere di distinguere i termini che sono più importanti per la rappresentazione logica di un particolare documento. Solitamente si usa la term frequency all'interno del testo. Ci sono alcune alternative:
\(f_{ij}\) : frequenza del termine i-esimo nel documento j-esimo;
\(f_{ij}\) normalized, essenzialmente divido la frequenza del termine nel documento per la frequenza massima presente;
\(f_{ij}\) log frequency:
in questo modo "smorzo" le differenze tra i valori di frequenza.
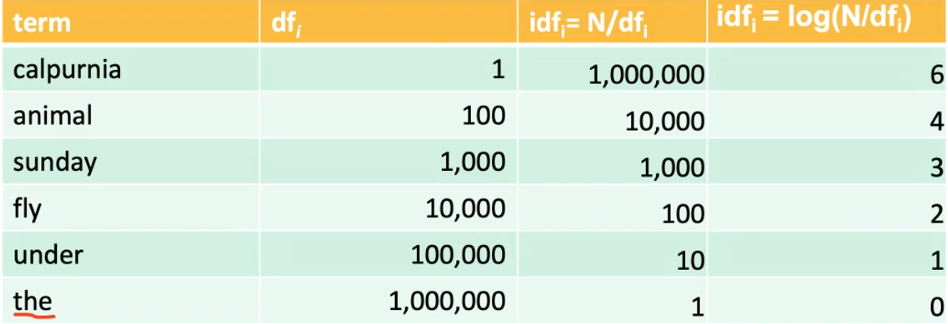
Altro fattore che si aggiunge al calcolo. L'idea è che i termini rari sono più informativi rispetto ai termini comuni.
Un termine raro è un termine presente in pochi documenti.
\(df_{i}\) --> in quanti documenti quel termine è presente
\(idf_{i}\) = \(\log(N/df_{i})\) --> indice di rarità del termine \(i\) all'interno della collection.
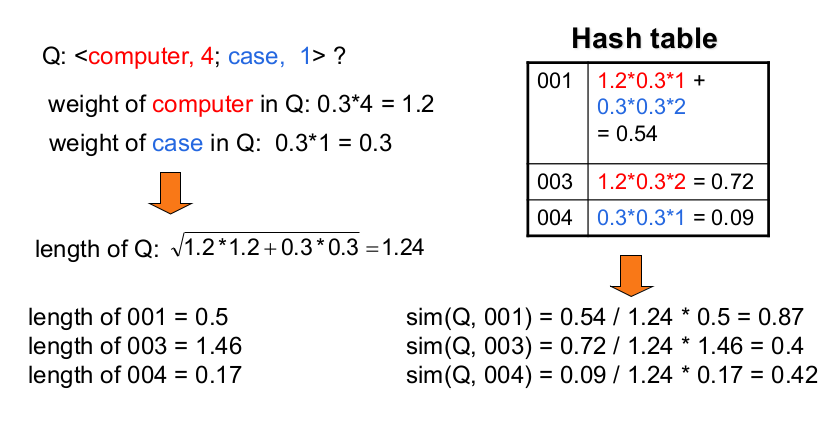
Mettiamo di voler assegnare un peso agli index term di queste due query:
"Arachnocentric": in questo caso l'idf non ha importanza;
"Capricious person": in questo caso l'idf di "Capricious" sarà molto più alto dell'idf di "person", che è un termine più comune;
Quindi il concetto è che verranno premiati i documenti che contengono i termini più rari che sono presenti anche nella query. Di conseguenza, per le query che contengono soltanto un termine, l'idf non ha influenza, perchè si moltiplica ogni volta per la stessa quantità.


Vantaggi
E' permesso l'ottenimento di documenti che approssimano la query;
Tali documenti sono ritornati in un ranking in base alla similarità;
La performance migliora nel complesso;
Svantaggi
Non c'è disambiguazione dei termini, non viene considerata la semantica;
Non viene analizzata la struttura della frase, quindi non è considerata la sintassi;
Non posso usare una matrice sparsa per effettuare i calcoli, che diverrebbero estremamente costosi dal punto di vista computazionale. E' necessario cercare un altra struttura dati con cui interfacciarsi.
La matrice di incidenza che è stata spiegata prima non è un'implementazione efficiente, dato che si tratta di una matrice sparsa, quindi in cui tendenzialmente compaiono pochi 1. Si usa quindi il solito inverted index! In particolare, si usa l'inverted index per trovare l'insieme dei documenti i quali contengono almeno una delle parole espresse nella query. Quindi se questa, ad esempio, contiene 3 termini, allora si deve accedere all'inverted index per 3 volte.
Supponiamo che in media un token di una query appaia in B documenti. Allora il retrieval time è \(O(|Q|B)\), molto meglio della ricerca che analizza tutti gli \(N\) documenti.
Il problema è che non si riesce subito a calcolare l'indice di similarity ,perchè non si ha una struttura dati che che lo permette. L'idea è quindi quella di costruire un'hash table in modo incrementale in cui si memorizza lo "score" di ogni documento. \(\Downarrow\)
Q \(\rightarrow\) query di input;
R \(\rightarrow\) Hash Table vuota;
Questa prima parte dell'algoritmo serve per memorizzare nell'hash table il numeratore delle similarity tra i vari documenti e la query. Il concetto è che si vuole cercare di "consumare" un token alla volta, massimizzando l'efficienza.
for each token T in Q: I = IDF of T # (log(total N of docs/n.of documents where token appears)) K = count of T in Q w = Weight of T in Q = I*K L = posting_list(T) # (each node has (i)doc ID and (ii) n.of occurences) O = occurence for each O in L: C = count D = document R[D] = R[D] + w_q * w_i = w * I * C

In questa parte viene calcolato il denominatore della similarità. In questi casi d'esempio la lunghezza della query si può calcolare, mentre si suppone di sapere la lungehzza dei documenti. Si veda l'esempio: \(\Downarrow\)
L = length(Q) # sqrt of sum of square of weights for D in R: (so for each document in hash table) S = R[D] # (numeratore) Y = length(D) simil(D) = S/(L*Y) # so L is same for each document