Modello probabilistico 10-11-22
L'idea che sta alla base del Modello Probabilistico è il determinare la probabilità che un documento sia rilevante rispetto ad una query fornita dall'utente. Si usano quindi dei tools statistici per effettuare delle stime e delle ipotesi. In particolare, definiamo la seguente variabile aleatoria:
\begin{align} & R_{d,q} = 1 \textrm{ se il documento d è rilevante per la query q} \\ & R_{d,q} = 0 \textrm{ otherwise} \end{align}In particolare, lo scopo è quello di ordinare i documenti secondo la loro probabilità di rilevanza, quindi secondo la probabilità che \(R_{d,q}\) sia = 1.
Il BIM (Binary Indipendence Model) è un modello probabilistico che si basa su due elementi:
L'indipendenza dei termini, quindi l'assenza della semantica;
L'assenza di pesi reali: semplicemente un termine può essere presente o meno all'interno di una query/documento. Quindi la rappresentazione logica di un documento \(j\) è questa:
Il tutto si basa sul Probabilistic Ranking Principle (PRP) \(\Downarrow\)
Se i documenti vengono ordinati efficacemente in base alla loro probabilità di rilevanza, allora l'efficienza del sistema è la migliore ottenibile.
E' necessario qundi definire una funzione che possa essere usata per ottenere i valori che poi andranno ordinati per stilare un ranking dei documenti per probabilità di rilevanza. Usiamo la similarità:
\begin{equation} sim(d_{j}, q) = \frac{\overbrace{P(R|\vec{d}_{j},\vec{q})}^\text{p. che il doc. sia rilevante per la query}}{\underbrace{P(\bar{R}|\vec{d}_{j}, \vec{q})}_\text{p. che il doc NON sia rilevante per la query}} \end{equation}Applicando la regola di Bayes \(\Rightarrow P(A|B)P(B) = P(B|A)P(A)\)
\begin{equation} \frac{\overbrace{P(\vec{d}_{j}|R,\vec{q})}^\text{p. di scegliere il doc. dal pool di doc.rilevanti R} \times P(R|\vec{q})}{\overbrace{P(\vec{d}_{j}|\bar{R},\vec{q})}^\text{p. di scegliere il doc. dal pool di doc. NON rilevanti} \times P(\bar{R}|\vec{q})} \end{equation}Dato che non si hanno informazioni a priori e che non influsicono sul ranking, i due termini a destra al numeratore e al denominatore possono essere semplificati.
Ora riscriviamo il numeratore e il denominatore, considerando che un documento in realtà è rappresentato come vettore di pesi binari.
Ciò significa che preso un documento dall'insieme di documenti rilevanti R, esso è proprio \(d_{j}\) se contiene tutti i termini presenti (\(w_{i,j} = 1\)) in \(d_{j}\) e NON contiene tutti i termini assenti (\(w_{i,j} = 0\)) in \(d_{j}\). Il ragionamento è analogo per il denominatore.

Ora, considerando la complementarietà delle probabilità e applicando la funzione logaritmo, si può riscrivere la formula come
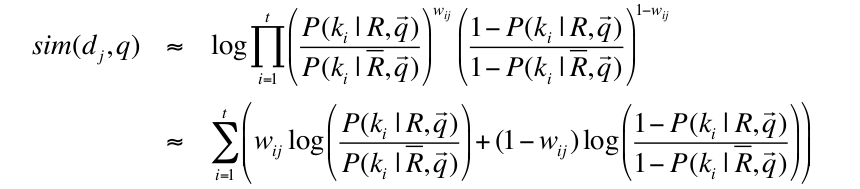
Si è essenzialmente portata fuori la produttoria, iterando su tutti i termini indistintamente. In questo modo, quando il termine è presente (\(w_{i,j} = 1\)) allora si considera solo la prima parte elevata alla \(w_{ij}\), dato che la seconda parentesi sarà elevata alla 0 quindi varrà 1. Al contrario, quando il termine NON è presente (\(1 - w_{i,j} = 1\)) allora alla produttoria contribuisce solo la seconda parentesi, elevata alla 1.
Si riscrive poi la formula usando le proprietà dei logaritmi. Si ottiene la seguente forma

Tramite questi passaggi intermedio:
\begin{equation} \sum_{i=1}^t (w_{ij}log(...)+log(...)-w_{ij}log(...)) \end{equation}si elimina il logaritmo centrale, essendo costante e si raccoglie \(w_{ij}\)
\begin{equation} \sum_{i=1}^{t} (w_{ij} (\log(...) - log(...))) \end{equation}si usano le proprietà dei logaritmi (differenza di logaritmi con base uguale) e si ottiene la prima delle due forme in figura. Si moltiplica ad ogni iterazione per \(w_{iq}\), dato che si vogliono considerare soltanto i termini presenti anche nella query. Infine si usano ancora una volta le proprietà dei logaritmi per la seconda delle due forme in figura.
Consideriamo ora la costante \(c_{i}\):

\(c_{i} = 0\) se un termine ha probabilità uguali di apparire in documenti rilevanti e non rilevanti;
\(c_{i} > 0\) se appare più probabilmente in documenti rilevanti;
Quindi essenzialmente per ogni documento si fa la sommatoria dei \(c_{i}\) per ogni termine \(i\) presente sia nel documento che nella query.
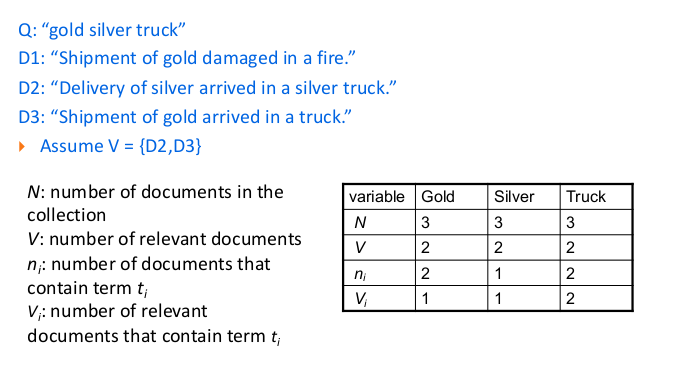
Prima di procedere con un'esempio di applicazione, c'è una nota da fare sulla probabilità iniziale. Infatti inizialmente non si conosce il pool R di documenti rilevanti per la query inserita dall'utente. Serve quindi un modo alternativo per calcolare i due termini fondamentali della formula, ossia \(P(k_{i}|\bar{R},\vec{q})\) e \(P(k_{i}|{R},\vec{q})\)
Si fa quindi un'assunzione iniziale: si suppone che i documenti rilevanti siano una piccola percentuale del pool totale, stabilendo che:
\(P(k_{i}|R,\vec{q})\) = 0.5;
\(P(k_{i}|\bar{R},\vec{q})\) = \(\frac{n_{i}}{N}\), si sono semplificati \(V_{i}\) e \(V\), essendo piccoli;
Dopo aver fatto ciò si applicano le procedure viste, e si ottiene un ranking iniziale dei documenti. Si prendono i primi \(V\) documenti e si considerano come pool di documenti rilevanti.
\(n_{i}\) è il numero di documenti che contengono il termine \(k_{i}\). A questo punto si hanno tutti gli elementi della formula:
\(P(k_{i}|R,\vec{q})\) = \(\frac{V_{i}}{V}\), dove \(V_{i}\) è il subset di V che contiene l'index term \(k_{i}\);
\(P(k_{i}|\bar{R},\vec{q})\) = \(\frac{n_{i}-V_{i}}{N-V}\);
Spesso si aggiungono degli offset per evitare divisioni per 0, per esempio:
\begin{equation} P(k_{i}|R,\vec{q}) = \frac{V_{i}+0.5}{V+1}; \end{equation}

Il concetto stesso di "probabilità di essere rilevante" è molto utile, e questo modello ne è un'implementazione chiara ed efficiente. Dall'altro lato, come al solito si considerano i termini indipendenti, senza guardare alla semantica dei contenuti. I pesi binari poi non considerano la frequenza con cui un termine compare all'interno di un documento. E' per questo che i BIM sono utili su corpus ristretti o in ambiti specifici. Un'altra variabile che influenza molto il ranking è il guess iniziale sul pool di documenti rilevanti, il quale può spostare di molto il ranking finale.
Tendenzialmente il vector model performa meglio del BIM probabilistico su corpus di documenti di natura generale.