Tolerant Retrieval
Appunti presi dalle lezioni dell'anno 2021.
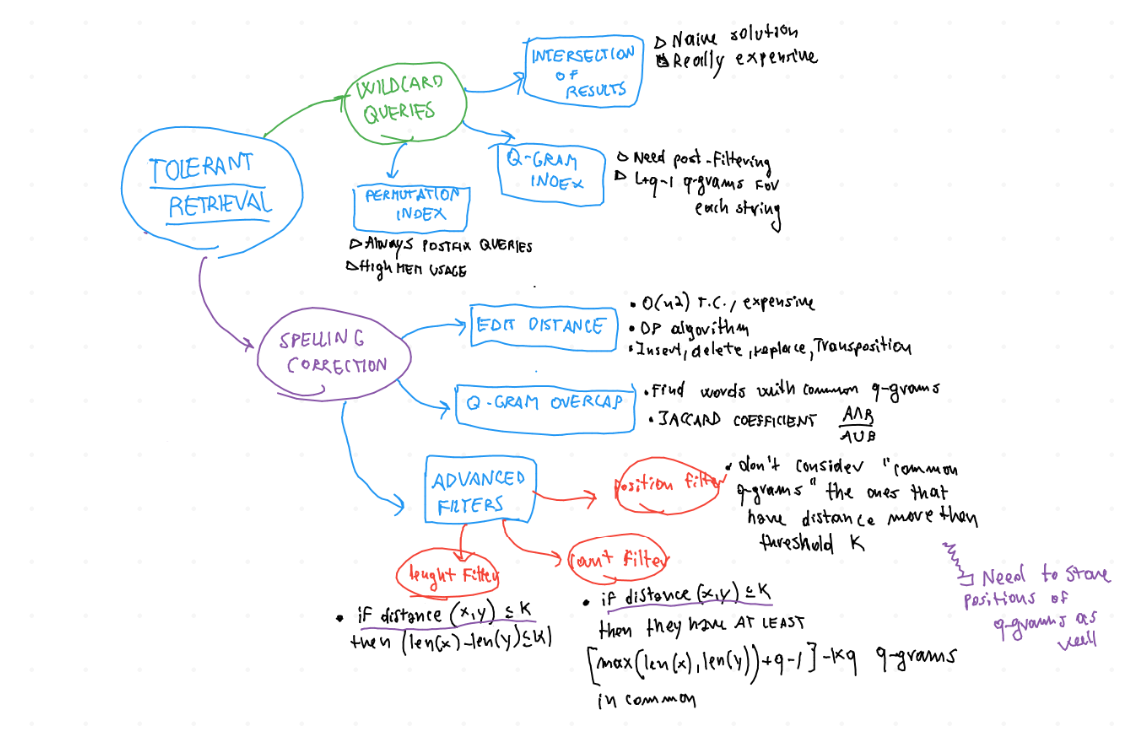
In generale, la Tolerant Retrieval si occupa della ricerca di documenti nei casi in cui le query fornite dagli utenti contengano parole che non sono presenti nell'indice. I tre casi presi in analisi sono wildcard queries, spelling correction e Soundex.
Per risolvere le wildcard queries si possono usare diversi metodi:
Intersection of results;
Permutation Index;
Q-grams Index;
A seguire i dettagli.
Le Prefix Query sono del tipo mon*.
Queste sono le meno problematiche, perchè la ricerca può essere fatta semplicemente nell'indice originario. Nello specifico, si effettua una ricerca binaria per trovare la prima parola che matcha, per poi scendere nell'indice ordinato.
Le Postfix Query sono del tipo *mon.
La soluzione piùsemplice è quella di mantenere in memoria un indice invertito: in questo modo si può ribaltare la query e effettuare una ricerca identica a quella per una prefix query.
Query tipo m*nchen.
In questo caso si possono adottare 2 soluzioni:
Intersection: facendo riferimento all'esempio, si fa una ricerca su m* e *nchen e si intersecano i set di risultati.
Permutation Index: si mantiene un'indice aggiuntivo che memorizza tutte le permutazioni di ogni parola nel dizionario, in cui ogni permutazione punta alla parola originale. "$" è semplicemente un carattere di terminazione aggiuntivo che viene memorizzato nell'indice insieme al resto della parola.
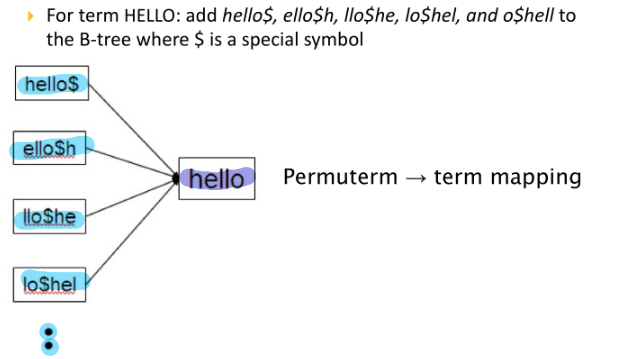Per processare una query si seguono poi le seguenti regole:
Per la ricerca ad esempio di hel*o, si cerca o$hel* Il segreto è cercare di ricondursi sempre ad una postfix query, non curandosi dell'ordine assoluto dei termini, ma soltanto di quello relativo. Il problema di questo approccio è la dispendiosità in termini di occupazione di memoria, che viene quadruplicata rispetto all'uso di un'indice normale.
q-gramma: sequenza di q caratteri della stringa a cui sono stati aggiunti \(q-1\) "#" all'inizio e \(q-1\) "$" alla fine.
Esempio per q = 3, per la parola "vacations":
{##v, #va, vac, aca, cat, ati, tio, ion, ons, ns$, s$$}
Quindi in generale da una stringa lunga \(L\) si ottengono \(L+q-1\) q-grammi. Data questa definizione, l'approccio per creare una struttura dati che possa permettere di effettuare Middle Queries è il seguente:
Generare tutti i q-grammi di ogni parola del dizionario;
Creare un'indice (q-gram index) in cui ogni q-gramma punta alle parole da cui può essere estratto.
Esempio di un bi-gram index \(\downarrow\)
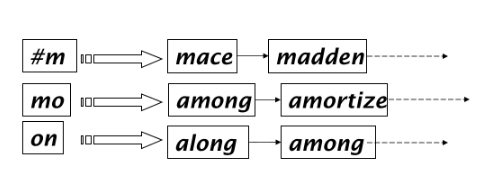
L'uso del q-gram index richiede un minor uso di memoria, dall'altro lato il permuterm index non richiede il post-filtering.
Usata per correggere i documenti inseriti nell'indice (raramente) o più spesso per correggere le query inserite dall'utente. Solitamente non viene corretto direttamente il documento, in pratica si cercano di correggere le parole che vengono salvate nell'index.
Per questo approccio, prima di procedere serve definire "da dove vengono prese" le parole corrette. Le due alternative sono:
Un generico dizionario linguistico;
Il lessico estratto dai documenti indicizzati;
In generale quindi l'idea è quella di calcolare un valore di distanza (inverso della similarità/similitudine) tra la parola da correggere e le possibili correzioni, per capire quali sono le più plausibili. Esistono diversi modi per fare questo calcolo:
Edit distance \(\rightarrow\) numero minimo di operazioni da effettuare per convertire una parola in un'altra.
Le operazioni consentite per convertire una parola in un'altra sono:
Modello Levenshtein: Insert, Delete, Replace;
Modello Damerau-Levenshtein: Insert, Delete, Replace, Transposition;
Per esempio:
\begin{align} & distance(dof, dog)=1 \\ & distance(cat, act)=2 \\ & distance(cat, dog)=3 \\ \end{align}invece considerando anche la trasposizione
\begin{align} & distance(cat, act)=1 \\ \end{align}perchè basta spostare la "c" dopo la "a". L'algoritmo che calcola questa distanza fa uso della DP, seguendo questi passi:
si inizializzano la prima riga e la prima colonna come in figura;
per riempire la tabella, quindi ad un generico passo:
se rosso == azzurro \(\rightarrow\) blu :=giallo;
altrimenti \(\rightarrow\) blu := 1 + min(giallo, verde);
il risultato finale è l'ultimo elemento in basso a destra;
Space complexity: O(n), basta memorizzare la colonna e la riga precedenti.
Time complexity: O(\(n^2\)), in quanto bisogna riempire l'intera tabella.
Esiste una variante di questo algoritmo che fa uso di una matrice aggiuntiva in cui sono memorizzati pesi per ogni coppia di lettere, in base alla loro distanza effettiva sulla tastiera. Ogni volta che si aggiungeva 1 nell'algoritmo, ora si aggiunge il peso corrispondente ai due caratteri presi in esame in quel momento. In questo modo alla fine si ottiene una distanza "pesata" che considera anche la probabilità di aver premuto un tasto rispetto ad un altro (ad esempio, il peso della coppia \(m,n\) sarà sicuramente minore del peso di \(m,q\), in quanto la sostituzione di \(m\) con \(n\) "costa meno" rispetto alla sostituzione di \(m\) con \(q\)).
Riassumendo:
quando un'utente digita una query, si calcolano le edit distance per tutti i termini nel vocabolario e si ritorna la parola con edit distance minore. E' comunque un'approccio lento dato che deve calcolare l'edit distance per molti termini.
L'idea è quella di calcolare i q-grammi della parola da correggere, per poi usare il q-gram index per trovare tutte le parole del lessico che condividono almeno 1 q-grama con la parola da correggere. Alla fine si mostrano soltanto le parole che hanno il maggior numero di qgrammi comuni.
in cui:
X \(\rightarrow\) q-grammi della parola da correggere;
Y \(\rightarrow\) q-grammi della parola del lexicon;
Il numeratore quindi rappresenta il numero di qgrammi comuni mentre il denominatore rappresenta il numero di qgrammi distinti totali. Rispetto all'edit distance, questo metodo consiste in un calcolo molto più semplice, lineare rispetto al numero di parole.
Se le liste di parole associate ai qgrammi sono mantenute in ordine alfabetico, basta uno scan lineare per trovare le parole che condividono \(x\) qgrammi.
Esistono alcuni filtri da applicare a priori alla parola da correggere e alle parole nel dizionario per evitare di calcolare l'edit distance. (Si cerca di calcolare l'edit distance per meno parole possibili).
Length Filter: si parte dal presupposto che se la differenza di lunghezza è pari a \(p\), allora l'edit distance della coppia di parole non può essere minore di \(p\).
Due stringhe \(S1\) e \(S2\) se hanno edit distance <= \(k\) allora abs(len(\(S1\))-len(\(S2\))) <= \(k\)
Count Filter: l'idea è che parole simili hanno in comune molti qgrammi
Due stringhe \(S1\) e \(S2\) che hanno edit distance <= \(k\) hanno almeno [max(len(\(S1\))),(len(\(S2\)))+ \(q\) - 1]-\(kq\) qgrammi.
Position Filter: si pensi alle seguenti sequenze di caratteri:
aabbzzaacczz
aacczzaabbzz
Queste generano (per \(q = 3\)) gli stessi identici q-grammi, ma in ordine diverso. Tuttavia queste parole hanno edit distance molto alta, pari a 4. L'idea del position filter è quella di memorizzare le posizioni dei q-grammi, e non considerare nel count filter i q-grammi che distano più di k posizioni.
Questo algoritmo serve per indicizzare le parole in base a "come suonano", in modo da creare degli insiemi di parole omofoniche. Ad alto livello, gli step da seguire sono i seguenti:
Trasformare ogni token in una sequenza di 4 caratteri tramite l'algoritmo;
Costruire un index usando queste forme ridotte;
Trasformare i termini della query;
Il processo di trasformazione in sequenze di 4 caratteri è il seguente:
