Gestione dell’informazione ITA-(2022/2023)
Cosa posso trovare qui?⌗
Questa pagina (in italiano) contiene i miei appunti del corso di “Gestione dell’informazione” del corso di laurea triennale in informatica di Unimore. Verranno quindi riportati gli approfondimenti/chiarimenti che vengono fatti durante le lezioni. Il materiale non è sostitutivo alle slide del corso.
→ Link per accedere al materiale didattico:
https://moodle.unimore.it/course/view.php?id=7287
Troubleshooting⌗
Se la pagina non carica correttamente i contenuti in latec, basta ricaricare la pagina
una o al massimo un paio di volte. Questo problema può essere legato alla grande
quantità di testo e immagini presenti in questa sezione.
(IR) TABLE OF CONTENTS⌗
- Information Retrieval vs Data Retrieval
- Text Operations
- Full Text Indexing
- Modelling
- Evaluation
- Tolerant Retrieval
- Ranking the Web
Information Retrieval vs Data Retrieval⌗
Già dal titolo del si può intuire la principale differenza tra le due discipline: nell’information retrieval il focus è sulle informazioni, mentre in basi di dati il focus è sui dati. Ciò significa che in I.R si lavora per soddisfare le esigenze informative dell’utente, che possono essere più o meno articolate e/o difficili da interpretare. Al contrario in basi di dati l’utente ha il compito di descrivere esattamente le sue necessità attraverso una query in linguaggio di interrogazione, la quale viene processata e vengono restituiti gli oggetti che “matchano” esattamente la richiesta. In information retrieval si lavora con corpus costituiti da documenti in linguaggio naturale, quindi si parla di dati non strutturati, mentre in data retrieval si lavora solitamente con database relazionali (quindi strutturati). L’output del sistema è molto diverso nei due casi:
- I sistemi di I.R puntano a restituire un ranking che sia il più pertinente possibile alle richieste dell’utente, cercando di restituire nelle prime posizioni documenti rilevanti;
- I sistemi di D.R restituiscono un pool di oggetti che semplicemente “matchano” la query inserita dall’utente.
Text Operations⌗
Document Processing⌗
-
Analisi lessicale: si converte una sequenza di caratteri in una sequenza di token, dei potenziali canditati per dei termini “index”. Questo compito viene eseguito dal lexer (es. GNU lex). -
Eliminazione delle stopwords: vengono eliminate quelle parole “inutili” che non danno informazioni per la ricerca, esistono elenchi appositi di stopwords per ogni lingua. -
Stemming e Lemmatization: esempio di uno stem –> ‘connect’ è lo stem di parole come ‘connected’, ‘connection’, ‘connecting’. Lo stemmer è il tool che si occupa della stemmization.Esistono alcuni parametri per giudicare uno stemmer: (i) correttezza, (ii) efficacia, (iii) miglioramento della performance.
esempio di un lemma –> ‘see’ è il lemma per ‘seen’ ‘saw’; Il lemmatizer si occupa della generazione dei lemma.
-
Selezione degli Indexvengono scelti i token più significativi (attraverso l’uso di parsers e taggers). Può essere fatta manualmente (da esperti) oppure automaticamente. Esempio: “Say” “Chair” “Be” “Enough” –> “Chair”. -
Parsing: processo di analizzare uno stream di dati input e verificare la sua correttezza sintattica. Questi strumenti (detti parser) lavorano sulla base di “banche dati” usando un approccio statistico. I parser analizzano l’intera struttura sintattica della frase e generano un’altra struttura dati che descrive il ruolo di ogni token (es. Abstract Syntax Tree). -
Tagging: processo che assegna alle parole il loro ruolo all’interno della frase.
(Verbo, Nome, Aggettivo, ecc…)
Thesauri⌗
Un Thesaurus è una lista di parole (sinonimi e contrari) importanti in un dato domain di conoscenza. Ad esempio, in ambito medico, alla parola “hand” potrebbero essere collegati concetti come “sanityzers”, “transplantation”, ecc.. A livello strutturale sono quindi dei dizionari che contengono associazioni.
Python NLTK, the basics⌗
In questo script vengono trattati i seguenti argomenti: (i) Generazione dei token, (ii) Rimozione delle stopwords, (iii) Lemmatizzazione, (iv) Stemming, (v) Tagging.
import nltk
from nltk.corpus import stopwords
from nltk.stem.porter import PorterStemmer
from nltk.stem.lancaster import LancasterStemmer
text = "This is a tests"
tokens = nltk.word_tokenize(text)
print(tokens)
# Stopwords removal and Lemmatization
wnl = nltk.WordNetLemmatizer()
# per stampare tutte le parole che non sono stopwords.
for t in tokens:
if not t in stopwords.words('english'):
print(wnl.lemmatize(t))
# --> ['This', 'is', 'a', 'tests']
# This
# test
# Stemming, using Porter and Lancaster, two popular stemmers
# They give the same output for easy input
porter = PorterStemmer()
print([porter.stem(t) for t in tokens])
lancaster = LancasterStemmer()
print([lancaster.stem(t) for t in tokens])
# POS tagging a list of lemmatizen tokens!
print([nltk.pos_tag([wnl.lemmatize(t) for t in tokens])])
# --> [[('This', 'DT'), ('is', 'VBZ'), ('a', 'DT'), ('test', 'NN')]]
Esercizio 1:
eseguire le seguenti operazioni: (i)Tokenization, (ii)Elimination of stopwords, (iii)Stemming, (iv) Selection of nouns su un file .txt contenente un libro di testo. In questo caso ho scaricato una copia locale del file, per semplicità.
import nltk
from nltk.corpus import stopwords
from nltk.stem.porter import PorterStemmer
path = "./book.txt"
file = open(path)
raw = file.read()
print(len(raw))
#step1: tokenization
tokens = nltk.word_tokenize(raw)
print(tokens[:20])
#step2: eliminate stopwords
no_stop_tokens = [t for t in tokens if not t in stopwords.words('english')]
print(len(no_stop_tokens))
#step3: stemming
porter = PorterStemmer()
stemmed_tokens = ([porter.stem(t) for t in no_stop_tokens])
#step4: get nouns thanks to tagging
tagged_tokens = (nltk.pos_tag([t for t in stemmed_tokens]))
print(tagged_tokens[:20])
nouns = [t[0] for t in tagged_tokens if t[1] == 'NN']
print(nouns[:20])
Wordnet (Thesaurus)⌗
Synset –> concetto, può essere rappresentato da più parole.
In un generico thesaurus sono chiamati Thesaurus Index Term.
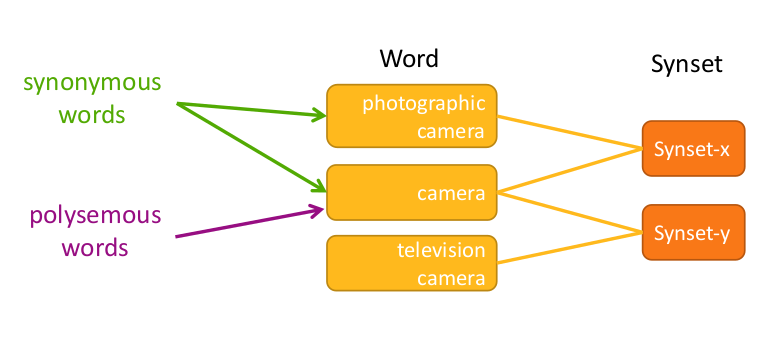
Wordnet mette a disposizione una serie di relazioni tra i synset, come i seguenti:
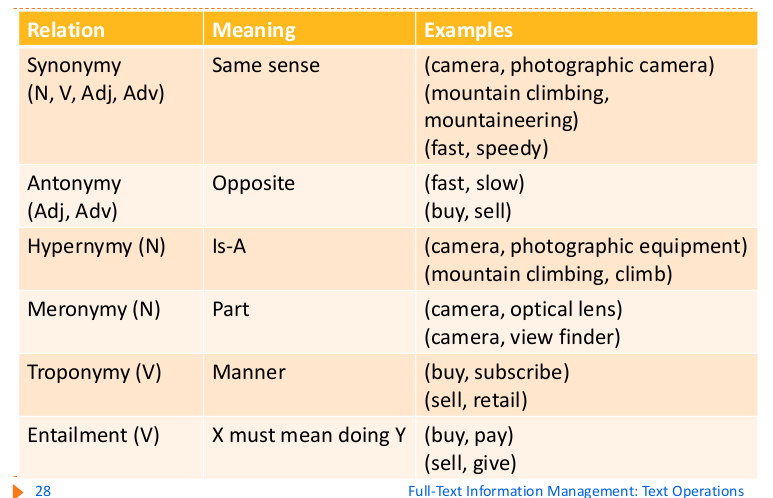
La relazioni solitamente più usate sono Hypernymy e Meronymy. Usare un thesaurus non è sempre una scelta corretta. In un search engine generico come google non ha senso, dato che il grafo delle relazioni diventerebbe enorme senza portare grossi benefici. Al contrario è molto utile in casi specifici (e.g. search engine per paper in ambito medico). Per corpus generici solitamente si usa un approccio più naive ma che comunque è efficiente: il bag of words (vedi dopo).
Word similarities⌗
sinonimia –> relazione binaria che lega due parole attraverso
il significato.
similarità o distanza –> metrica più “loose” per dare un gradiente
di similarità.
Queste relazioni non vanno confuse con le relazioni del thesaurus. Ad esempio benzina e macchina potrebbero essere collegate nel thesaurus ma potrebbero anche non essere sinonimi!
Come misurare la similarità tra concetti (tramite l’uso di un thesaurus)? (i)path based (ii)information content measures.
- Path based: sfrutto la gerarchia di ipernimia per stabilire il “livello” di somiglianza di due concetti. Esistono principalmente 2 formule per effettuare il calcolo: (i) path distance similarity, (ii) Wu-Palmer similarity.
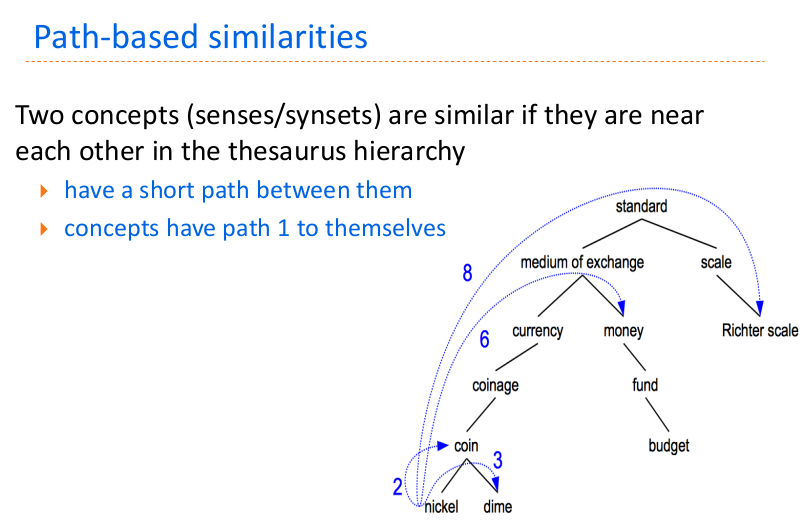
Path distance similarity:
\begin{equation} sim_{path-distance}(c_{1}, c_{2})= \frac{1}{ShortestPath(c_{1}, c_{2})+1} \end{equation}
Wu-Palmer similarity:
\begin{equation} sim_{Wu-Palmer}(c_{1}, c_{2})= \frac{2*depth(LCS(c_{1},c_{2}))}{depth(c_{1})+depth(c_{2})} \end{equation}
Il problema della prima formula è che è molto discontinua e genera dei valori non ben distribuiti. Questo problema viene risolto da Wu-Palmer con la loro formula. Per chiarezza, LCS –> Least Common Subsumer.
-
Information content mesaures: quanto spesso questi concetti vengono usati nello stesso contesto. Dato un concetto, definisco con P(c) la probabilità che scelta una parola a caso in un corpus rappresenti il determinato concetto.
Information content: Può essere interpretato come il livello di sorpresa di un particolare concetto. Questo indice infatti è alto quando c’è un synset “raro” o “inaspettato”.
\begin{equation} IC( c) = -log P( c) \end{equation}
Similarità di Resnik: calcolo l’information content del
least common subsumer. Due concetti sono molto simili se
si incontra raramente un termine il cui senso è comune tra i
due.
\begin{equation} sim_{resnik}(c_{1}, c_{2}) = -log(P(LCS(c1,c2))) \end{equation}
Word Sense disambiguation⌗
La WSD consiste essenzialmente nell’assegnare il senso corretto ad ogni istanza di una certa parola di interesse.
- Determinare tutti i sensi che quella parola può assumere: abbastanza automatico usando un thesaurus;
- Analizzare il contesto dove la parola compare.
- Bag of words: il contesto è rappresentato da un pool di parole “vicine” al termine di interesse che vengono estratte.
- Relational information: approccio più complesso che estrae altri parametri come la distanza.
Ecco un’approccio per implementare il tutto:
for each noun N, for each sense Sn of N:
compute confidence Csn in choosing sn as sense of N
select sense with higher confidence
Ora la domanda è: come calcolo la confidence \(C_{s_{n}}\) ?
\(\rightarrow\) mi baso sulla similarità tra \(s_{n}\) e tutti gli altri sensi delle parole nel contesto! Poi per calcolare la similitudine posso usare tecniche come la path-based, già discussa in precedenza. Testualmente può anche essere espresso nel seguente modo: Voglio cercare di trovare il senso della parola S che “fitta” meglio nel contesto di riferimento, che è costituito da molte parole, anch’esse legate a molti sensi.
Ricapitolando, ecco lo pseudocodice dell’algoritmo:
max_confidence = 0
for each Si synset di I:
confidence = 0
for each J term in context:
max = 0
for each Sj synset of J:
similarity = simil(Sj, Si)
if(similarity > max):
max = similarity
confidence += max
if(confidence > max_confidence):
max_confidence = confidence
pick(synseth_with_confidence(max_confidence))
Codice effettivo di un semplice word sense disambiguator in python:
def disambiguateTerms(terms):
for t_i in terms: # t_i is target term
selSense = None
selScore = 0.0
for s_ti in wn.synsets(t_i, wn.NOUN):
score_i = 0.0
for t_j in terms: # t_j term in t_i's context window
if (t_i==t_j):
continue
bestScore = 0.0
for s_tj in wn.synsets(t_j, wn.NOUN):
tempScore = s_ti.wup_similarity(s_tj)
if (tempScore>bestScore):
bestScore=tempScore
score_i = score_i + bestScore
if (score_i>selScore):
selScore = score_i
selSense = s_ti
if (selSense is not None):
print(t_i,": ",selSense,", ",selSense.definition())
print("Score: ",selScore)
else:
print(t_i,": --")
Query Expansion⌗
Esercizio sull’espansione di query. Proposta di algoritmo / soluzione:
import nltk
from nltk.corpus import stopwords
from nltk.stem.porter import PorterStemmer
from nltk.corpus import wordnet as wn
def disambiguateTerms(terms):
selected_syns = []
syns_defs = []
for t_i in terms: # t_i is target term
selSense = None
selScore = 0.0
for s_ti in wn.synsets(t_i, wn.NOUN):
score_i = 0.0
for t_j in terms: # t_j term in t_i's context window
if (t_i==t_j):
continue
bestScore = 0.0
for s_tj in wn.synsets(t_j, wn.NOUN):
tempScore = s_ti.wup_similarity(s_tj)
if (tempScore>bestScore):
bestScore=tempScore
score_i = score_i + bestScore
if (score_i>selScore):
selScore = score_i
selSense = s_ti
if (selSense is not None):
selected_syns.append(selSense)
syns_defs.append(selSense.definition())
return selected_syns, syns_defs
def expand_query(syns):
res = []
for s in syns:
for l in s.lemmas():
res.append(l.name())
return res
raw = input ("Insert query: ")
tokens = nltk.word_tokenize(raw)
nostokens = [t for t in tokens if not t in stopwords.words('english')]
tagged_tokens = (nltk.pos_tag([t for t in nostokens]))
pool = [wn.morphy(x[0]) for x in tagged_tokens]
print(pool)
selected_syns, syns_def = disambiguateTerms(pool)
expanded_query = expand_query(selected_syns)
print(expanded_query)
Full Text Indexing⌗
Introduzione⌗
Solitamente un indice è appropriato quando:
- Ho molti dati da gestire;
- Quando ho un pool di dati semi-statico, quindi può essere aggiornato periodicamente ma non supporta frequenze troppo alte.
Gli index più usati sono (i) inverted index, (ii) suffix array, (iii) signature files. Ovviamente si cercano sempre di capire i costi di accesso, di costruzione e di aggiornamento.
- \(n\) –> dimensione in byte occupati dal testo;
- \(m\) –> lunghezza del pattern che voglio cercare;
- \(M\) –> byte disponibili in memoria principale;
TrIe⌗
(prefix tree) Indice che memorizza stringhe, per velocizzare la ricerca e altre operazioni.
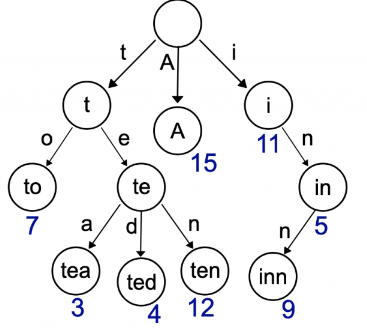
Costo di ricerca di una parola: \(O(m)\), quindi lineare rispetto al numero di caratteri della parola che sto cercando.
Inverted Index⌗
L’idea è quella di memorizzare, per ogni termine \(t\), una lista di tutti i documenti che contengono quella parola. Ecco le componenti pricipali di un inverted index:
Vocabolario–> insieme di tutte le parole contenute nella collezione di documenti. Per ogni parola viene mantenuta come informazione il numero di documenti in cui quella parola è presente (document frequency).Posting List–> mantiene le informazioni riguardo alla precisa locazione delle singole parole. Esistono due tipi di posting list:- Document based: esempio –> car:11 (4) –> viene indicato in che documento compare la parola e con quale frequenza.
- Word based: ho la locazione della parola di interesse nel documento, a livello posizionale.
Qui sotto sono illustrati degli esempi di record che potrebbero essere presenti in un inverted index. Notare come la document frequency coincida con il numero di caselle presenti nella posting list. Questo è il caso in cui la posting list sia Document based. Se fosse Word Based, ovviamente i nodi della posting list sarebbero più ingombranti: invece della frequenza all’interno del documento, sarebbero indicate le precise posizioni delle istanze.
| Index term | df | posting-list-couple | posting-list-couple |
|---|---|---|---|
| computer | 2 | \(D_{7},4\) | \(D_{8},2\) |
| Index term | df | posting-list-couple | posting-list-couple | posting-list-couple |
|---|---|---|---|---|
| database | 3 | \(D_{1},2\) | \(D_{2},3\) | \(D_{3},2\) |
Lo space requirment del vocabolario è abbastanza esiguo: esiste una legge che
descrive il suo andamento chiamata Heaps law. L’andamento è \(O(n^{b})\) con \(b \in [0,1]\)
Ovviamente la grandezza del vocabolario dipende da tutto il preprocessing che
viene fatto, quindi da come vengono generati i token e come vengono filtrati.
Il costo di memorizzazione dell’inverted index è generalmente \(O(n)\):
- Per i document based, è circa il 20%-40% della dimensione del testo;
- Per i word based, è il 40% senza stopwords e l'80% con le stopwords;
Costruzione di un Inverted Index⌗
Solitamente la costruzione si basa sulla memorizzazione del vocabolario in un trie. Dopo aver fatto il preprocessing si seguono i seguenti step:
- Leggere la parola del testo
- Cercare la parola nel trie
- Se non è presente, viene aggiunta, altrimenti viene aggiornata la lista delle occorrenze di quella parola.
Costo: \(O(n)\), dove n è la somma dei token da indicizzare. Normalmente l’inverted index viene diviso in due file, per dividere il dizionario dalle posting list. Questo perchè il dizionario viene caricato in memoria principale, mentre le posting list rimangono in memoria secondaria e vengono accedute mediante degli offset. Nel file del vocabolario vengono memorizzate le parole, e per ogni parola un puntatore alla propria lista all’interno del posting file. Ecco un’esempio di entry all’interno di un vocabulary file:
- “start” indica l’offset di inizio della lista;
- “n” indica la lunghezza della lista corrispondente;
| Term | Start | n |
|---|---|---|
| science | 7 | 3 |
Quando devo usare il vocabolario, in che struttura dati conviene caricarlo per velocizzare la ricerca? Per chiarezza: il trie di cui parlavamo prima viene usato in fase di costruzione, per facilitarla. Una volta finita la fase di costruzione, il file con il vocabolario viene memorizzato e il trie non serve più. Rimane quindi da capire quale sia la struttura più efficiente in cui caricare, in seguito, il vocabolario.
- Sorted Array –> ricerca binaria \((log(n))\). L’inserimento è costoso, dato che può comportare lo shifting degli elementi all’interno della struttura.
- B+ Tree –> veloce e efficiente ma comporta spazio extra, richiede la gestione di una struttura dati aggiuntiva.
- Trie
- Hash
Ricerca⌗
Boolean Retrieval
La boolean retrieval è semplice concettualmente, basta ottenere i risultati (insiemi di documenti )
dei singoli elementi e combinarli usando l’apposito operatore booleano (unione, intersezione, ecc…).
Per quanto riguarda il processing dell’operando AND, si può usare un semplice algoritmo di “merging” per risolvere il problema. Ad esempio, si supponga di voler cercare tutti i documenti che contengono entrambe le parole “computer” e “science”. In tal caso, supponendo che le due posting list contengano gli ID dei documenti in maniera ordinata, basta un’approccio a due puntatori per risolvere il problema in \(O(n)\).
- \(p1\) –> puntatore al primo elemento della posting list di “computer”, che contiene la lista (ordinata) di documenti in cui compare la parola;
- \(p2\) –> puntatore al primo elemento della posting list di “science”;
answer = []
while p1 != NULL and p2 != NULL:
if (doc_ID(p1) == doc_ID(p2)):
answer.append(doc_ID(p1))
else if doc_ID(p1) < doc_ID(p2):
p1 = p1->next;
else
p2 = p2->next;
return answer;
Phrasal Retrieval
Spesso è interessante sapere, ad esempio, in quali documenti e in che posizione appare una determinata frase, quindi una sequenza di parole. Ad esempio, si può essere interessati a capire in che posizione e in quali documenti appare la stringa “computer science”. Come intuibile, non basta sapere se in un documento appaiano entrambe, serve anche controllare che esse siano contigue (in questo caso). Per eseguire in maniera efficiente questa operazione è opportuno avere un inverted index word based. Si seguono i seguenti passi:
- Si crea una lista di documenti che contengono enrambe le parole, come visto nel paragrafo precedente.
- Si selezionano, uno alla volta, tutti i documenti di questa lista;
- Per ogni documento, si creano \(n\) vettori, dove \(n\) indica il numero di parole della frase (nel caso dell’esempio, \(n=2\)); Ogni vettore contiene tutti gli indici di apparizione di quella parola in quel documento;
- Si cercano le tuple corrette all’interno dei vettori. Nell’esempio, si vogliono individuare tutti gli indici \(i\) tali che \(Computer_{i}+1 = Science_{j}\)
Vettore delle apparizioni di “Computer” nel documento \(D_{1}\) \(\downarrow\)
| i=0 | i=1 | i=2 | i=3 |
|---|---|---|---|
| 4 | 8 | 12 | 44 |
Vettore delle apparizioni di “Science” sempre nel documento \(D_{1}\) \(\downarrow\)
| i=0 | i=1 | i=2 | i=3 |
|---|---|---|---|
| 6 | 9 | 32 | 45 |
In questo caso, la frase “computer science” compare agli indici 1 e 3, perchè i valori corrispondenti sono contigui! Ecco lo pseudocodice, da applicare ad ogni documento \(d \in D\):
- \(P\) = insieme di tutti gli array del documento corrente;
- \(k_{i}\) = keyword i-esima;
- \(P_{i}\) = array delle apparizioni di \(k_{i}\);
- \(P_{s}\) = array delle apparizioni più corto;
- \(k_{s}\) = keyword che compare meno volte;
In questo caso, si intende semplicemente ritornare la lista dei documenti che contengono la frase cercata.
- (p+i-s) \(\rightarrow\) si aggiunge alla posizione \(p\) all’interno dell’array, la distanza tra \(i\) (indice all’interno della frase della parola su cui si sta facendo la binary search) e \(s\) (indice all’interno della frase della parola di riferimento). Essenzialmente quindi si aggiunge la distanza tra la parola di riferimento e la parola di cui si sta cercando l’occorrenza.
for each position p in Ps:
for each keyword ki != ks: # per tutte le altre keyword della frase
use BinarySearch to find a position (p+i-s) in Pi
if correct position for each keyword found, add d to answer # d is current document
else try with next position, going on with loop
return answer
Questo procedimento è da iterare su ogni documento che contiene tutte le parole di riferimento, per capire se compaiono nell’ordine corretto.
Modelling⌗
- 📃 Lezione 02-11-22 e 03-11-22 (Modello Vettoriale)
- 📃 Lezione 10-11-22 (Modello Probabilistico)
- 📃 Lezione 17-11-22 (Modelli Fuzzy e Okami BM25)
Evaluation⌗
- 📃 Lezione 07-12-22 (Retrieval Evaluation)